치토스 선배 강의 듣고 씀.
희소 테이블(sparse table)
희소 테이블(sparse table)은 배열 내 구간의 쿼리를 빠르게 수행할 수 있는 자료구조이다.
배열 arr[0, ..., N-1]이 아래와 같이 있다고 가정하고,

i ~ j 구간에 대한 쿼리의 결과(예를 들어 구간 합)를 function(i, j)라고 두면 우선 sparse table 배열 d[i][0]에는 function(i, i) = arr[i]가 들어간다. 그 후 d[i][k]에는 function(i, i + 2^k - 1)이 들어간다. 이를 표로 그리면 아래처럼 된다.

즉 d[1][3]에는 1번 원소부터 시작해서 2^3 = 8개 원소의 합이 저장되어 있다.
만약 2~7 구간의 합을 구하고 싶다면, 이는 2~5 구간의 합 + 6~7 구간의 합과 같으므로 d[2][2] + d[6][1]로 구할 수 있다.
시간복잡도는 전처리 O(NlogN), 쿼리 당 O(logN)이다. 이럴 경우 세그먼트 트리를 쓰는 것과 시간복잡도 면에서 크게 다를 것이 없다🙄.
sparse table 유용하게 쓰기
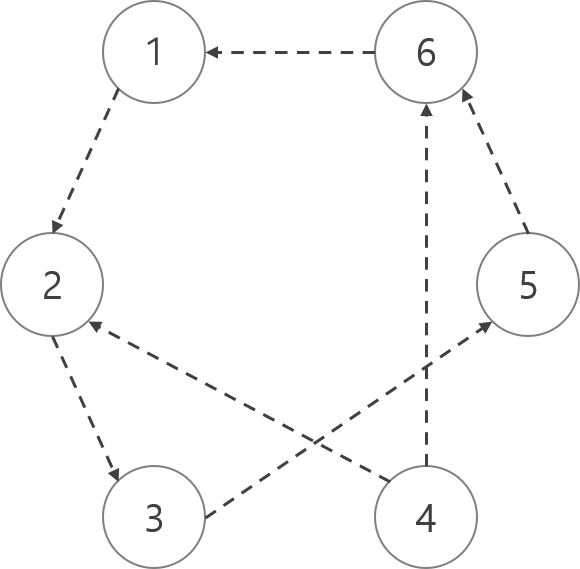
위와 같은 방향 그래프가 있다고 하자. 1번 노드에서 1번 이동하면 2번 노드로 가고, 1번 노드에서 10번 이동하면 다시 1번 노드로 온다. 이정도는 계산이 쉬운데, 만약 그래프나 쿼리 수가 엄청 커서, 193403번 노드에서 389734번 이동한 결과를 134178번 물어보면 조금 화가 날 것이다. 그럴 때 sparse table을 사용하면 좋다. 만약 i번 노드에서 k번 이동한 결과를 알고 싶을 경우에는 k = a0 * 2^n + a1 * 2^(n-1) + a2 * 2^(n-2) + ... + an * 2^0 (a0~an은 0 or 1)인 a0~an을 찾아서 계산해주면 된다.
for (int j = 1; j < 19; j++)
{
for (int i = 0; i < M; i++)
{
d[i][j] = d[d[i][j - 1]][j - 1];
}
}
전처리는 이렇게 해주고
int query(int n, int x)
{
int index = x;
for (int i = 18; i >= 0; i--)
{
if (n & (1 << i))
index = d[index][i];
}
return index;
}
쿼리는 이렇게 처리해주면 된다. 와!
쿼리 O(1)만에 하기
얘를 이용하면 쿼리를 O(1)만에 할 수 있는 상황들이 있다.
예를 들어 구간합이 아니라 구간 내 최댓값을 구할 때를 생각해보자!

1~6 구간의 최댓값을 구한다고 가정할 때, 우리가 가지고 있는 값인 1번부터 2^2개 구간 중 최댓값과 3번부터 2^2개 구간 중 최댓값을 이용해 구할 수 있다. 중간에 겹치는 구간이 있어도, 어차피 최댓값을 구하는 중이기 때문에 괜찮다.

이렇게, K개 구간 중 최댓값은 i번부터 2^m개, j번부터 왼쪽으로 2^m개의 sparse table 값을 통해 알 수 있다. 이 때 m은 [밑이 2인 logK]이다.
코드로 짜보자.
for (int i = 0; i < N; i++)
{
mx[i][0] = arr[i];
}
sparse table 배열 mx의 각 열 당 0번 원소는 arr[i]로 초기화해준다.
for (int j = 1; j < lg[N] + 1; j++)
{
for (int i = 0; i < N; i++)
{
if (i + (1 << j) > N)
break;
mx[i][j] = max(mx[i][j - 1], mx[i + (1 << (j - 1))][j - 1]);
}
}
mx 배열을 채워준다. (lg[K]에는 미리 밑이 2인 logK값을 저장해놓는다.) i번째부터 2^j개의 원소의 최댓값은, i번째부터 2^(j-1)개의 원소의 최댓값과 i + 2^(j-1)번째부터 2^(j-1)개의 원소의 최댓값 중 큰 값일 것이기 때문에 식을 저렇게 짜준다.
int query(int l, int r)
{
int len = r - l + 1;
int m = lg[len];
int res = max(mx[l][m], mx[r - (1 << m) + 1][m]);
return res;
}
이후 쿼리는, 구간의 길이를 이용해 m값을 정하고, 미리 저장되어있는 i부터 2^m개, j부터 왼쪽으로 2^m개의 결과값 중 큰 값으로 반환하면 된다. 쿼리당 O(1). 최고!
관련 문제
[BOJ] 합성함수와 쿼리
17435번: 합성함수와 쿼리
함수 f : {1, 2, ..., m}→{1, 2, ..., m}이 있다. 이때 fn : {1, 2, ..., m}→{1, 2, ..., m}을 다음과 같이 정의하자. f1(x) = f(x) fn+1(x) = f(fn(x)) 예를 들어 f4(1) = f(f(f(f(1))))이다. n과 x가 주어질 때 fn(x)를 계산하는 ��
www.acmicpc.net
[BOJ] LCA 2
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정�
www.acmicpc.net
'Algorithm > Data Structure' 카테고리의 다른 글
| [자료구조] 트라이(Trie) (0) | 2023.05.18 |
|---|---|
| [자료구조] 세그먼트 트리(Segment Tree) (0) | 2020.04.14 |
| [자료구조] 큐(Queue) (0) | 2019.11.11 |
| [자료구조] 스택(Stack) (2) | 2019.11.03 |
 tokki
tokki
댓글