선배 강의 듣고 씀.
세그먼트 트리에서 업데이트는 O(logN)의 시간 복잡도를 가진다.
그런데 업데이트가 노드 하나하나가 아니라 구간으로 주어질 때, 그걸 일일이 업데이트를 해주면 느릴 수 있다.
그래서 구간 업데이트가 들어올 때마다 그걸 바로 적용해주지 않고, 업데이트가 있다는 내용을 따로 저장해놓고 나중에(lazy) 해당 노드를 방문할 때 처리한 후 자식 노드로 업데이트를 전파(propagation)해주는 방식이 lazy propagation이다.
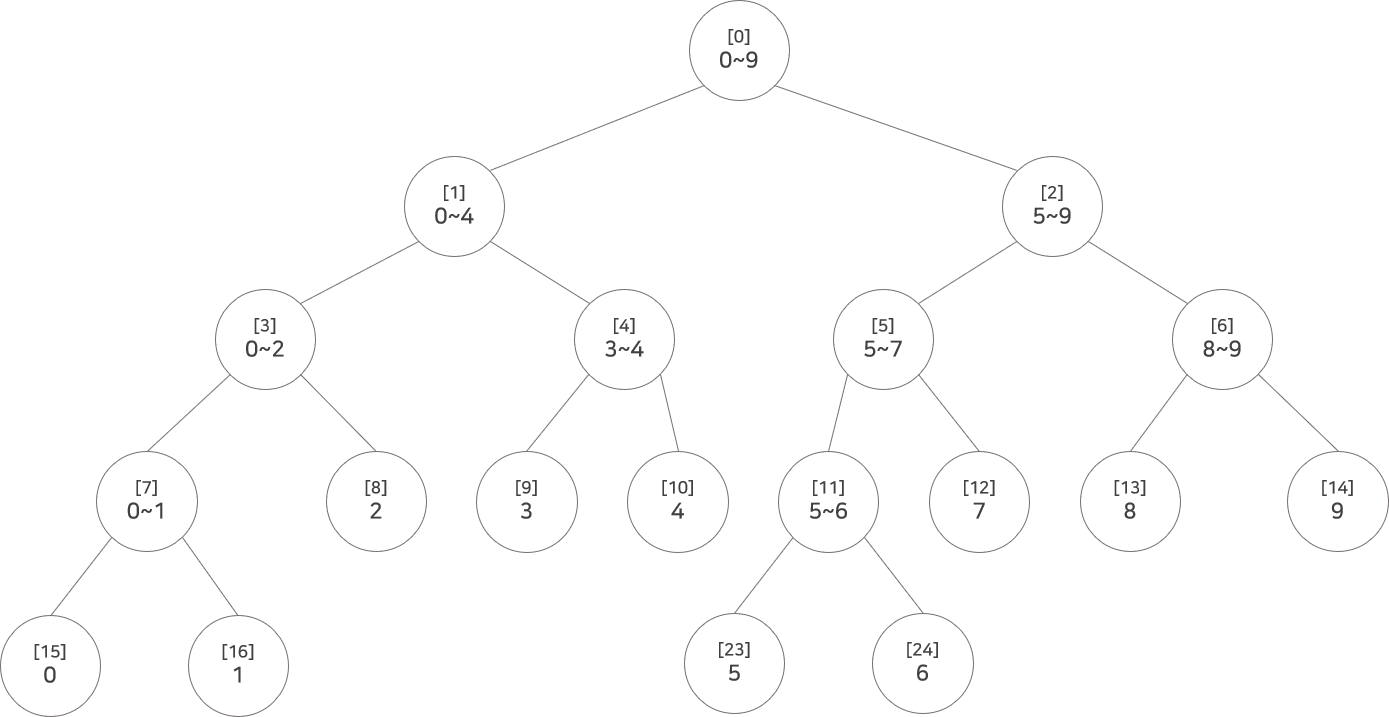
이런 세그먼트 트리가 있을 때, 2~7 구간에 업데이트를 준다고 가정해보자.

일반적으로는 8, 9, 10, 23, 24, 12번 노드에 접근해서 위 부모 노드들까지 값을 업데이트시켜줄 것이다. 이런 식으로 하면 만약 업데이트되는 구간이 더 길어질 경우 시간복잡도가 최대 O(NlogN)까지 늘어날 것이다.
2~7번 구간의 값을 찾을때를 생각해보면 이 때 접근하게 되는 노드는 8, 4, 5번 노드인데 이 노드들과 조상 노드들의 값만 업데이트해주고, 자식 노드들에는 '이런 업데이트가 있다'라는 것을 알려주고 실제로 업데이트를 하지는 않을 것이다.
예를 들어 이게 구간합이 들어있는 세그트리라고 가정하면, +n이라는 업데이트가 있을 때 4번 노드는 2개짜리 구간이므로 +2n을 해주고, 5번 노드는 3개짜리 구간이므로 +3n을 해준다. 8번 노드는 리프노드이므로 그냥 +n을 해주기만 하면 된다. 그 후에 자식 노드가 있다면 자식 노드들에 +n을 해야한다는 것을 알려준다. 이걸 lazy값이라고 한다.

3~6 구간에 대한 쿼리(구간합 등)가 들어왔을 때, 값을 찾기 위해 0, 1, 4, 2, 5, 11번 노드를 방문하게 될 것이다. 4번 노드에는 이미 최신값이 들어있으므로 그냥 그 값을 사용한다. 그리고 11번 노드에는 lazy값이 있다. 위에서랑 똑같이 11번 노드에는 +2n하고, 자식 노드들에는 lazy값을 전파시킨 후 11번 노드의 lazy값은 없앤다.

결론적으로 9, 10, 23, 24, 12번 노드들에는 업데이트되어야 할 값들이 있지만, 실제로 그 노드들에 있는 값을 수정해주지는 않았다. 대신 '업데이트 해야 한다' 라고만 알려주고 다른 업데이트나 쿼리를 통해 이 노드에 방문했을 때 실제로 이 값들이 적용될 것이다.
관련 문제
[BOJ] 구간 합 구하기 2
10999번: 구간 합 구하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄��
www.acmicpc.net
'Algorithm > Algorithm' 카테고리의 다른 글
| [알고리즘] 허프만 코딩 (0) | 2021.12.16 |
|---|---|
| [알고리즘] 좌표 압축 (2) | 2020.10.09 |
| [C++] max_element(), min_element() (0) | 2020.04.29 |
| [알고리즘] 카데인 알고리즘(Kadane's algorithm) (0) | 2020.04.25 |
| [알고리즘] 비트마스크(Bit Mask) (0) | 2020.04.16 |
 tokki
tokki
댓글